How many gallons of water would it take to get to the Moon?
We replaced rocket fuel with good ole H2O.
Hey! You! Don’t forget to subscribe if you haven’t already.
The only way to get anywhere is to leave something behind. As existential as that statement is it’s true—both in our personal lives and the physical world. In physics, this statement translates to Newton’s Third Law: For every action there is an equal and opposite reaction. If you push on a wall, the wall pushes back. If you’re on a jet ski, the only way to move forward is to push water backward. Today we’re going to use these same principles to help us determine if it would be worthwhile to swap our boring old rocket fuel with water.
Rockets use momentum to go up. They accelerate and push hot gas downward to gain speed upward. Momentum is just this equation:
1 and 2 are the two objects. For us 1 is the rocket and 2 is the gas. V is the object’s velocity and m is its mass. It suffices to say that the rocket weighs a lot more than the gas. Therefore, to get meaningful speed in the rocket, we need to get the gas movin’—fast. In real life, we get this gas up to speeds in excess of Mach 11 (8,500 mph). [1]
This equation, however, is a bit tough to work with. In physics, it’s a lot easier to work with forces. Because of this, we differentiate the equation (calculus!) to get them. Force is momentum per second.
With forces, we can start to understand how our rocket will move. But before we go any further we’re going to have to understand some space talk: namely “Delta-V’. This is how much you need to change your speed to get where you need to go. Imagine you’re driving in your car and you want to go a mile. Your delta-v is the speed you need to get up to so that you can throw it in neutral and coast to your destination. Now obviously it isn’t that simple on the road because air resistance will slow us down but in space, there’s nothing to resist you. So that’s how we do it with rockets—we get up to speed and cut the engines and let whatever speed we’ve given ourselves get us to our destination. That’s why, when you watch a rocket launch, it fires its engines for just minutes at a time and coasts for hours, days, even weeks after you turn the engine off. This saves fuel and increases the amount of payload we can carry.
In practice, delta-v has a bit more complexity to it, but conceptually that’s all it is. The speed you need to get yourself to in order to get where you want to go. That being said, how do you find it? And how does it relate to the water we want to use as fuel? This question is answered by integrating the last equation. Force is equal to mass times acceleration. And acceleration is velocity per second. So to turn the left-hand side from acceleration to velocity, we have to integrate. And in doing so we get Tsiolkovsky’s equation:
V(e) is the velocity of the exhaust out of the rocket, m(i) is the rocket’s initial weight, and m(f) is the rocket’s weight when it runs out of fuel. At first glance, there are no real differences in using water vs. rocket fuel. As long as you use the same amount, and eject it at the same speed, your delta-v should be the same. And because water is denser than rocket fuel, you may even save on cargo space! But alas, upon further inspection we notice a pretty large difference: water is a liquid, and rocket fuel, after being combusted, is a gas. And those two have very different properties. Simply put for our application: you can’t move water nearly as fast as you can a gas.
The fastest that I’ve been able to find water moving is in waterjet cutters. These tools shoot a jet of water so fast they can literally cut steel. Can we reasonably scale this technology up to our rocket? Definitely not. But we’ll press on in the name of science. These waterjet cutters get the water going up to speeds of Mach 3 (1,000 m/s—2200 mph). Recall that the speed of normal rocket exhaust is around Mach 11. So that being said, let’s see how it compares.
We’ll substitute the empty (without fuel) weight of a SpaceX Falcon 9 rocket (25,600 kg). This represents our rocket when it runs out of fuel. V(e) is the maximum water velocity of Mach 3 and delta-v is the average delta-v it takes to get to the moon: ~15.93 km/s. Plugging this all into the rocket equation above we get a required initial mass of 467 billion pounds of water. That’s just shy of 85,000 Olympic-sized swimming pools. You would need 670 fully loaded oil tankers to haul this much water—that’s 100,000 times more propellant than the Saturn V rocket used to get the Apollo astronauts to the moon.
This may be a bit weird to you, and it was to me, because how can a 4x decrease in exhaust speed lead to a 100,000x increase in propellant needed. That’s because the solution to the rocket equation has an exponential term, which makes the relationship look like this: [2]
This shows that, as you need more delta-v, the required fuel grows exponentially. And at a certain point, you either need to find a way to increase how fast you eject your propellant, or you need to try a new one altogether. This goes to show why we need such intense rocket engines as is, and why usually 90%+ of a rocket’s weight is fuel. Like we said earlier, to get anywhere in this universe you have to leave something behind. And in the case of the Moon, we have to leave a lot—especially when you try to use water to get you there.
Thank you for reading this week’s edition of It’s Not Rocket Science, I hope you enjoyed it. Look out for next week’s newsletter and in the meantime, don’t forget to subscribe!
Check us out on social media!
Check out last week’s newsletter here.
For more details…
Cover Image: https://www.fabbaloo.com/2020/05/rocket-crafters-tests-star-3d-3d-printed-rocket-engine
[2] https://en.wikipedia.org/wiki/Tsiolkovsky_rocket_equation






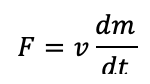


Matthew, you amaze me.