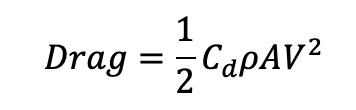Santa - Why and How

If Santa really wanted to pull it off, what would it take? An analysis.

Dec 24, 2020

Welcome to the first edition of “It’s Not Rocket Science”, an aerospace themed newsletter here to answer common questions and bizarre hypotheticals. Please enjoy the inaugural letter and reach out if you have more ideas! Happy holidays.

-Matt

Santa might have bitten off a bit more than he can chew. He’s got a lot of houses to hit and not a whole lot of time to do it. He’s got magic on his side, but what if he didn’t? If Santa actually wanted to pull off this scheme everyone says he does, what would it take? Is it actually possible?

Let’s start by understanding the actual size of the earth. It’s pretty massive, obviously, but we’ve got ways of getting around it. For the average person, the most sensible choice would be to fly commercial. Currently, the longest commercial flight is operated by Singapore Airlines, which has a nonstop service from Singapore to Newark, NJ on an Airbus A350. This flight covers just over 9,500 miles and lasts 18 and a half hours. [1] To put that into perspective, the equatorial circumference of the Earth is 24,900 miles. [2] Therefore, you would need to take this flight over 2 and a half times to fully circle the globe, which amounts to over 48 hours of nonstop flying. This estimate assumes that you’re taking off and landing, which you would have to do, because otherwise the plane would run out of fuel. If this A350 could refuel midair, which is common for military aircraft but not for commercial, then it would be faster. The A350’s cruise speed is Mach 0.85, which at altitude corresponds to about 560 mph. [3] At this speed, without stopping, it would take 44.5 hours to circle the globe. This saves some time but doesn’t quite cut it to deliver the presents. We have to get faster.

Staying on Earth, the next step would be to go military and supersonic. The most famous supersonic military jet is the SR-71 Blackbird. This aircraft clocks in at over 2000 mph when flying at altitude (85,000 ft). [4] At this speed, Santa could get around the Earth in under 12.5 hours, again given midair refueling. This would work for his scheme, as he technically has 24 hours of darkness. This seems like a good choice, so we’ll run with it.

The first problem is it would be pretty hard to drop presents accurately from 85,000 ft. Not only would they be obliterated when released at 2000 mph, but it would also be impossible to time dropping them perfectly. Let’s do the math. In high school physics, almost everyone learns how to figure out the trajectory of a ball once you throw it. This might trigger some bad memories but bear with me. The image below shows this notorious problem. You throw a ball at some angle, theta, and with some velocity, V. How far does it go?

This can be solved by looking at the position and velocity of the ball at any time, t, using the following equation for both horizontal and vertical motion. This is where the simplification comes in, because in those classes you were told “not to worry about air resistance”. Drag from the air imposes a force, and corresponding acceleration, on the ball. We won’t worry about that for now.

In this case, the motion in the horizontal direction has a constant speed and no acceleration, because it was thrown and then left alone. Because of this, in the horizontal direction, the position of the ball is simply:

Where Sx(0) is the initial position, 0, and Vx is the velocity of the ball in the x (horizontal) direction. This works for the horizontal, but what about the vertical?

Vertically there is acceleration, and it’s due to gravity. This acceleration is constant everywhere on the surface of the Earth, and it is 9.81 m/s^2 (32.17 ft/s^2). This is why, when you drop something, it falls. Without air resistance, every object accelerates by this amount when dropped on Earth. Some of you may have seen the astronaut dropping a hammer and a feather on the moon. The moon has gravity, not the same amount as Earth (because it’s much smaller), but unlike Earth it has no air resistance. So, when dropped, the two objects with different weights fall at the same speed. (If you’re interested check out this video) Therefore, the ball’s acceleration is non-zero, and the velocity changes with time. Which intuitively makes sense. The ball starts with some positive vertical velocity, and slowly that vertical velocity goes to zero as the ball reaches its peak. Then that velocity increases downwards until it hits the ground. So, in this case, the velocity equation becomes:

Where Vy(0) is the initial vertical velocity of the ball, and ay is the vertical acceleration, in this case, -32.17 ft/s^2. This value is negative because we defined our positive y axis as upwards, and this acceleration pulls the ball downwards. Subsequently, the position equation becomes:

Using these three equations, if we’re given a time, t, we can solve for the x and y position of the ball. We can apply this same thought process to the presents. When they are dropped, they start at some vertical height and with a horizontal velocity equal to that of the sled. Gravity pulls them downwards and they follow a similar arc pattern.

To see where the presents will go once dropped, however, we must consider air resistance. This is where these equations get hairy, because the drag force felt by an object is defined by the equation below:

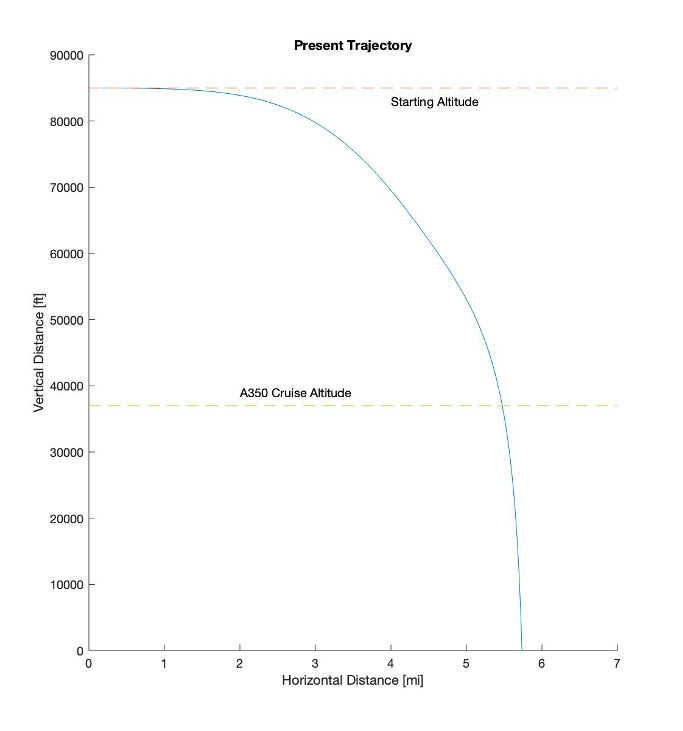
Cd is the coefficient of drag, which is just based on how aerodynamic the object is. Rho is the air density, A is the characteristic area (don’t worry about this for now, just think of it as the relevant surface area hitting the air), and V is the velocity that the object is traveling at. Not only does this mean that the acceleration of the present is changing with time, it’s also changing with the present’s velocity. This results in a system of equations that is unsolvable. To know the position at a time, t, we must know the acceleration, which requires us to know the velocity, which requires us to know the acceleration… This loop continues, making this problem “analytically” unsolvable, meaning it can’t be solved directly. Not to mention the fact that we must consider changes in air density with altitude. However, using numerical integration techniques in Matlab, this problem becomes more manageable. Sparing you all the details, a rough estimate for the true trajectory of the presents gives the figure below.

For anyone that is overly curious, this analysis assumes the present is a cube with edge length 1 ft and mass of 10 lbs.

At first glance, this seems very precise: Santa has to drop the present when he is 5.74 miles from the target, to be exact. However, at this speed, a delay of just one second in drop timing results in the following trajectory, putting the present over half of a mile off course.

Working backwards, we can find the kind of margin that Santa has to work with. Most chimneys nowadays couldn’t fit any sort of present, let alone a jolly animal anti-activist, but for the sake of argument, we’ll assume a large, old school chimney with a square stack 2 feet by 2 feet. Praying for a lucky bounce, the code can be used backwards to find the time delay that Santa is afforded. This results in a window of just under 0.7 milliseconds–yes, milliseconds. The average blink takes 400 milliseconds. Not to mention that over a residential neighborhood, with a linear distance between houses of 50 feet, Santa has to drop one present every 17 milliseconds just to hit every house. At this point, he should be pouring out presents willy-nilly. If this already seems unlikely to happen, he might not even be able to get off the ground.

Forgetting about the issue of actually dropping off the presents, what kind of wings would Santa need on this sled to be able to lift all of this? Note that this is only if you don’t subscribe to and/or are skeptical of the whole “magic” idea. Let’s look at the Airbus A350, which is a larger commercial aircraft used for overseas flights. This aircraft has a maximum payload capacity of 150,000 lb, which is A LOT. [3] That’s about 43 Toyota Camrys. There are aircraft, however, that can carry much more. The Russian-built AN-225 cargo aircraft has a maximum payload capacity of 500,000 lb. [5] The new PS5 weighs around 10 pounds, so we’ll assume this is a reasonable weight for the presents that Santa is dropping. (hint hint Santa) Already some quick math shows that this massive aircraft, which has a wingspan of 290 ft, could only hold enough PS5’s for 50,000 people. That’s plenty for any other purpose, but for ours and Santa’s, that’s not going to cut it. We need bigger wings.

That’s the AN-225, that thing is huge. [5] Lift produced by wings can be found very similarly to drag, with the following equation:

Again, CL is the coefficient of lift, which is experimentally found and has to do with the shape of the wing. Rho is the air density, S is the area that provides lift, and V is the velocity the aircraft is flying at (more exactly, the relative velocity of the air over the wing). This equation already shows a glaring relationship, because we’re flying so high, the air density is much lower than what we experience on the ground, less than 3% as dense. This means we need to be flying very fast to make up for it, which thankfully we are. In order to cruise at a constant speed, the lift that the aircraft creates must equal its weight. In our case, everything is a constant, known value except for the wing area, S.

To upscale the sled to accommodate presents for say, the whole city of New York, which is currently at about 18.8 million people, the sled would have to be able to carry 188 million lbs of presents. In addition to this, the sled needs fuel and a frame to support these presents. Using a similar ratio to the AN-225, where the total weight is about 2.8 times the payload weight, the total weight of the sled goes up to 526 million lbs. Using the equation that we developed earlier, with a CL of 0.6, which is the highest you can reasonably get while flying level, the wing area would need to be 3 million square feet, that’s 108 square miles, or 4.7 times the land area of Manhattan. Already this sled would need to be as big as the city it’s attempting to deliver presents too. Let’s just stick to magic. (Note here that we are not taking into account compressibility effects that arise from flying 3 times the speed of sound)

In conclusion, Santa is full of it. Even with the speed of the fastest jet aircraft in human history, the precision of a B-2 bomber, the present-slanging capabilities of a literal mini-gun (@ me for details), and wings the size of, well, West Virginia, Santa’s sled could only hit houses on the equator. The facts are lining up against him, so I propose that there’s only one thing left to do: Cancel Santa. The bit has gone long enough, and so has this one.

I hope you learned at least a little bit about Aerodynamics in this newsletter as well as the power and sadness that Matlab is capable of generating. If any of the topics above were not explained enough, or explained in too much detail, please reach out and these can be addressed in future letters. Thank you for reading!

It's Not Rocket Science

Discussion about this post